

So now (correct me if I'm wrong), but I just subtracted the two and got -1.8855 (see the other number was so small the difference barely changed). A unit vector is a vector with a length of one (unitless) which points in a defined direction. A third way to represent a vector is with its unit vector multiplied by a scalar value called its scalar component. And once we subtract ((-9.23sin40)-(10sin45)) and multiply that also by 0.145 kg (mΔv), we get -1.8855. A vector representing an object’s weight has a vertical reference direction and downward sense or negative sense, for example. Another change is that since the ball bouncing off is considered in the -y direction, we would make 9.23sin40 to -9.23sin40. For the y component, we would carry out the same task, but instead, we would switch the cos out for a sin.

Example 6 (LiveMath) Test Your Knowledge Force couples appear in many problems, and they represent a practical way for applying moments on a body.
#MOMENT VECTOR 2D FREE#
So then we would subtract Vf-Vi and then multiply by the mass (mΔv remember) meaning that we should get -6.93x10^-5 or -6.93E-5. It is important to realize that a couple moment is a free vector meaning that it can be shown at any point on the body as long as its magnitude and direction are not altered. And since the ball is moving right on the plane, the question says that that is positive. To find the initial, we would just change the numbers accordingly. And with the triangle being a right triangle, we can simply do 9.23cos40. So we take 9.23 m/s and now have to find the x component in the triangle. To find Δpx, we have to use the mΔv formula, but to find Δv, we need to carry out trig function.
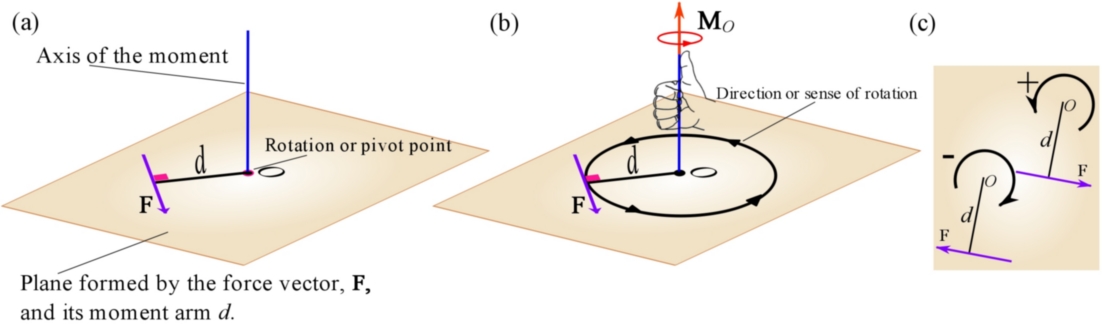
The only way we can find the Δp is if we fine Δpx and Δpy and add them together (or subtract correct me if I'm wrong, but in this problem the way doesn't really matter, you'll see why). Starting off, we need to know what Δpx is and what Δpy is, because to find the force on the ball we can use the impulse-momentum theorem and say that FΔt=mΔv. We can define the moment of inertia of a 3D object about the three coordinate. Consider a two-dimensional (2D) displacement vector in the x-y plane, with magnitude Delta r. The answer I got was slightly off by 10N but the process should be similar. a straight line segment drawn in space in the direction of the vector. 4) Moments add together as vectors, so the total moment is: Example. No idea if this is relevant anymore but why not. Calculating the moment in 2-D using components: 1) Select a positive direction (CCW.


 0 kommentar(er)
0 kommentar(er)
